本記事では、サイコロの出目の期待値が正しいのかどうかを調べるために、プログラムで求めてみて確認した結果をまとめています。
サイコロの出目の期待値をプログラムで求めた
サイコロを振った時の出目の期待値
サイコロを振った時に出る目の期待値は、約3.5です。計算式は以下の通りです。
$$E=1*\frac{1}{6}+2*\frac{1}{6}+3*\frac{1}{6}+4*\frac{1}{6}+5*\frac{1}{6}+6*\frac{1}{6}=3.5$$
これは期待値を求める公式で求めたわけですが、実際に正しいのかどうか分からないので、実験してみました。
実験の概要
・サイコロを1つ振って出た目を記録する
・出た目の平均を求める
・試行回数を100万回にすることである程度確率が収束するようにする
ソースコード
import matplotlib.pyplot as plt
import random
appearances = []
try_num = 1000000 #試行回数
for i in range(try_num):
appearances.append(random.randint(1,6))
# 平均の計算
average = sum(appearances) / len(appearances)
print(average)
#プロットエリアを確保
plt.figure()
plt.subplot(1,2,1)
#出た目の確率密度関数を表示
plt.hist(appearances, bins=100)
filename = "hist.png"
plt.savefig(filename)
#それぞれの目の出る確率を計算
rate = []
for i in range(1,7):
rate.append(appearances.count(i) / try_num)
plt.subplot(1,2,2)
plt.pie(rate,labels=rate)
plt.show()
実行結果
出力されたサイコロの目の平均値は以下のようになった。
3.495992
サイコロを振った時に出る目の期待値は3.5なのでほぼ等しいですね。ただし、出目が偏っているなどサイコロの出目が異常な場合はこの実験は意味がないので、ちゃんとそれぞれの出目の確率が等確率になっているかを調べます。
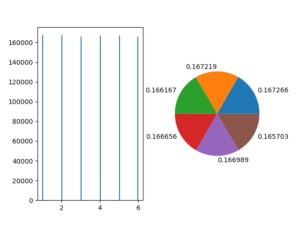
出力されたグラフ
それぞれの目が出る確率
上の2つのグラフはサイコロのそれぞれの出目が出る確率を表しています。
グラフによると、それぞれの目の出る確率がほぼ等しく、約16%になっていることがわかります。
結論
サイコロを振ったときに出る目の期待値は、約3.5で正しいことが分かりました。
また、サイコロの出目は1~6が等確率で出ていることが分かりました。